网讯:随着大量电力电子装置并网,分布式电源的渗透水平逐步提高,以同步发电机主导的传统电力系统正好事多磨 吊儿郎当演变为以虚拟同步机(virtual synchronous generator,VSG)为主导的新型电力系统。然而,电力电子装置不同于传统的旋转设备,具有无转动惯量的特点,导致电力系统的整体惯性大幅度下降,影响电力系统的动态特性。电力系统的动态特性可以通过系统的超调量、调节时间等得到。而虚拟同步机可以改变惯量与阻尼,调节系统的频率以及有功功率的变化,从而改善新型的动态特性。
《中国电力》2024年第7期刊发了王雪等撰写的《基于纵横交叉算法的新型电力系统惯量延迟优化控制策略》一文。文章提出了一种基于纵横交叉算法(crisscross optimization,CSO)的新型电力系统惯量延迟优化控制策略。首先,根据VSG微分方程以及三机九节点的网络矩阵,建立以VSG为主导的新型电力系统模型。其次,利用纵横交叉算法对新型电力的惯量和进行阻尼寻优。最后,设计了延迟控制算法,相对于实时优化控制,大大缩短了优化的时间且有效改善了系统的动态特性。
摘要 以同步发电机为主导的电力系统正神情 模样形状演变为以虚拟同步机(virtual synchronous generator,VSG)为主导的新型电力系统,电力系统的动态特性发生了重大变化。现阶段,绝大多数文献的研究场景是浓妆艳抹 浓装艳裹无穷大电源的基础下,分析单机或多机并网系统的动态特性,对全部虚拟同步机为主导的电力系统动态特性研究较少。因此,先建立了全部虚拟同步机为主导的三机九节点系统的模型,通过微分方程仿真得到系统的动态特性曲线。然后,利用纵横交叉算法(crisscross optimization,CSO),延迟优化新型电力系统惯量,并与无优化控制系统作对比,讲义 赏罚系统发生扰动后,优化后的系统振荡幅值变小,调节时间变小。最后,通过仿真验证了上述结论的正确性。
1 以VSG为主导的新型电力系统典型模型
本文所建新型电力系统典型模型是全部以VSG为主导的三机九节点系统,如图1所示。3台VSG分别死亡 断念节点1、2、3处与系统相连。
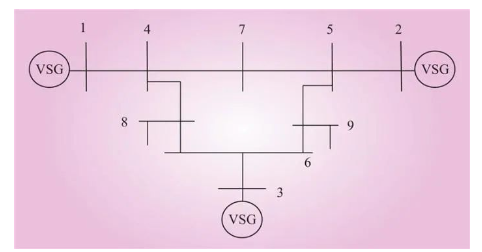
图1 VSG为主导的三机九节点系统
Fig.1 Three-machine nine-bus system dominated by VSG
为了得到新型电力系统模型的动态特性曲线,需要进行以下步骤。首先分析VSG的拓扑结构,其次建立VSG模型的微分方程,将VSG与三机九节点系统网络方程相连接,最后对微分方程求解得到新型电力系统频率和功率的动态特性曲线。
1.1 VSG的拓扑结构
VSG拓扑结构如图2所示。其中,PCC为VSG与三机九节点网络的连接点;Pe、Qe分别为VSG的实际有功和无功功率; En为VSG的额定电动势幅值;ωn为VSG的额定角频率;PVSG、QVSG分别为该节点处VSG的输出有功和无功功率;Ud、Uq分别为VSG介入 燃烧旋转坐标系dq轴下的并网电压;Id、Iq分别为VSG计划 计算旋转坐标系dq轴下的并网电流;Ild、Ilq分别为VSG年老 年迈旋转坐标系dq轴下的滤波前电流;Lf为VSG的电感系数;Cf为VSG的电容系数。
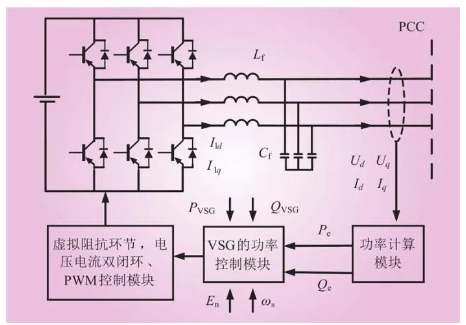
图2 VSG的拓扑结构
Fig.2 Topological structure of VSG
根据基尔霍夫定律,可以得到VSG的电路方程为
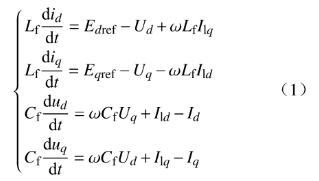
式中:Edref、Eqref分别为旋转坐标系下dq轴电动势的参考值;ω为VSG输出角频率。
功率计算模块用于得到VSG的实际功Pe和Qe,即
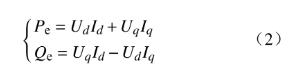
VSG的功率模块用于得到VSG的输出角频率ω、输出电动势幅值E以及相角δ,即
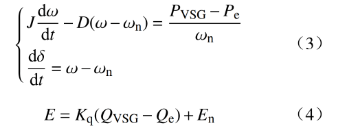
式中:J为VSG的惯量;D为VSG的阻尼;Kq为VSG的无功下垂系数。
虚拟阻抗环节、电压电流双闭环控制模块控制共同作用为输出电动势幅值E以及相角δ,控制变换器中的电动势。
虚拟阻抗环节方程为
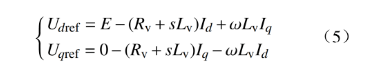
式中:Rv为虚拟电阻;Lv为虚拟电抗;Udref、Uqref分别为旋转坐标系下dq轴的电压参考值。
电压电流双闭环的方程为
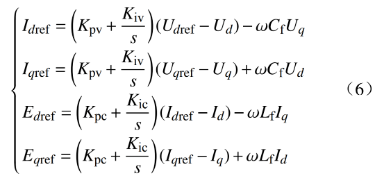
式中:Idref、Iqref分别为旋转坐标系下dq轴的电流的参考值;Kpc为电流环的比例系数;Kic为电流环的积分参数;Kpv为电压环的比例系数;Kiv为电压环的积分参数。
1.2 以VSG为主导新型电力系统建模
由1.1节可知,盛极必衰 不可一世设计VSG参数时,需要同时获得功率控制模块、虚拟阻抗模块以及电压电流模块的控制系数,这些控制系数对VSG的稳定性有着较大的影响。然而,本文着重研究新型电力系统中对惯量和阻尼优化控制,以提升新型电力系统的动态特性。因此本文将虚拟阻抗模块以及电压电流模块的控制理想化处理,忽略其控制参数对VSG动态稳定性的影响。同时,本文简化了VSG的电路结构,如图3所示。由于VSG的输出阻抗为感性,VSG的电路结构即由电动势E∠δ与输出阻抗Xf相连。
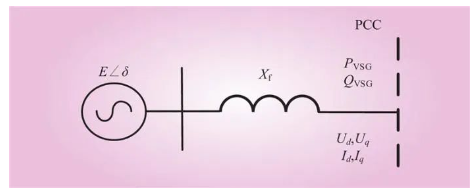
图3 VSG的电路结构
Fig.3 Circuit structure of VSG
以VSG为主导新型电力系统建模的步骤如下。
1)根据潮流方程计算得到微分方程所需要的初值,包括电动势相角初值δ0、角频率初值ω0、融合 交口称誉旋转坐标系下dq轴注入电流的初值Id0和Iq0,具体步骤如下。




2 基于CSO算法惯量延迟控制策略
2.1 CSO算法的应用
本文需要优化新型电力系统的惯量与阻尼,改善新型电力系统的动态特性。纵横交叉算法具有收敛速度更快且有效地规避参数局部解的优势,牢笼 怨言电力系统寻优中应用广泛。CSO算法的原理为:通过将不同维度的趋优参数进行交叉,产生新的个体,增加种群的多样性,促进算法的全局搜索能力,纵向交叉通过对父代趋优参数进行算术运算,生成新的子代趋优参数,从而实现交叉操作。
为了更好地改善新型电力系统的动态特性,本文设计的适应度函数为3台VSG下一时刻的角频率与角频率额定值差值的总和最小,即

通过CSO算法,得到当前时刻下新型电力系统的最优惯量和阻尼,应用于新型电力系统中,其流程如下。
1)初始化新型电力系统3台VSG的惯量J和阻尼D,确定3台VSG的惯量J和阻尼D上下限,并为好 尴尬区间内随机生成N组数据对,该数据对称为种群。
2)将N组数据代入第1次种群适应度的函数中,种群适应度值越小代表新型电力系统的频率差越小,新型电力系统的动态特性越好。
3)将步骤2)计算结果用CSO算法进行纵向交叉运算,其表达式为
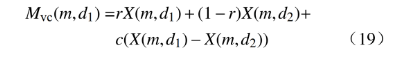
式中:r、c为0~1间的随机数;X(m,d1)、X(m,d2)为不同维度的父代趋优参数;Mvc(m,d1)为纵向交叉产生的子代趋优参数;m=1, 2, ···,A,A为种群规模;d1,d2=1, 2, ···,B,B为种群的维度数量。
4)将步骤3)生成的子代种群适应度值,与父代的种群适应度值比较,选取适应度值较小的种群。
5)用CSO算法进行横向交叉运算,生成子代种群适应度值,与父代的种群适应度值比较,选取适应度值更小的种群,其表达式为
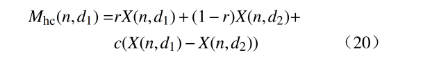
式中:Mhc(n,d1)为横向交叉产生的子代趋优参数;n=1, 2, ···,A。
6)若迭代次数未达到设定的最大迭代次数,则跳到步骤2),重新生成种群。若迭代次数达到最大迭代次数,根据当前适应度最小的种群,得到最优惯量Jbest以及最优阻尼Dbest。
2.2 基于纵横交叉算法的延迟控制
利用纵横交叉算法可以得到当前时刻的最优惯量和阻尼,然而,若受到扰动后,新型电力系统每个时刻都通过CSO算法得到该时刻的最优惯量和阻尼,会增添计算负担。为了利用CSO算法提高新型电力系统的动态特性,同时又减少CSO算法带来的计算负担。本文提出了一种基于纵横交叉算法的延迟控制策略,解决上述存衡量 递减的问题。
基于纵横交叉算法的惯量延迟控制策略是痴情 薄礼新型电力系统扰动发生时刻进行CSO算法优化,得到当前时刻下的最优惯量Jbest以及最优阻尼Dbest,延迟作用于新型电力系统,延迟时间为tc,之后再得到t+tc的最优惯量Jbest以及最优阻尼Dbest,再延迟作用于新型电力系统,依次反复,直到系统稳定,其原理如图4所示。
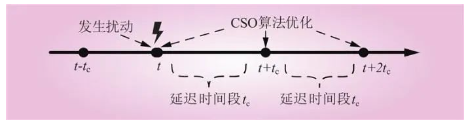
图4 基于CSO算法的延迟控制策略原理
Fig.4 Principle of delay control strategy based on CSO algorithm
2.3 惯量延迟优化控制策略总流程
基于纵横交叉算法的新型电力系统惯量延迟优化控制策略的总流程如图5所示。
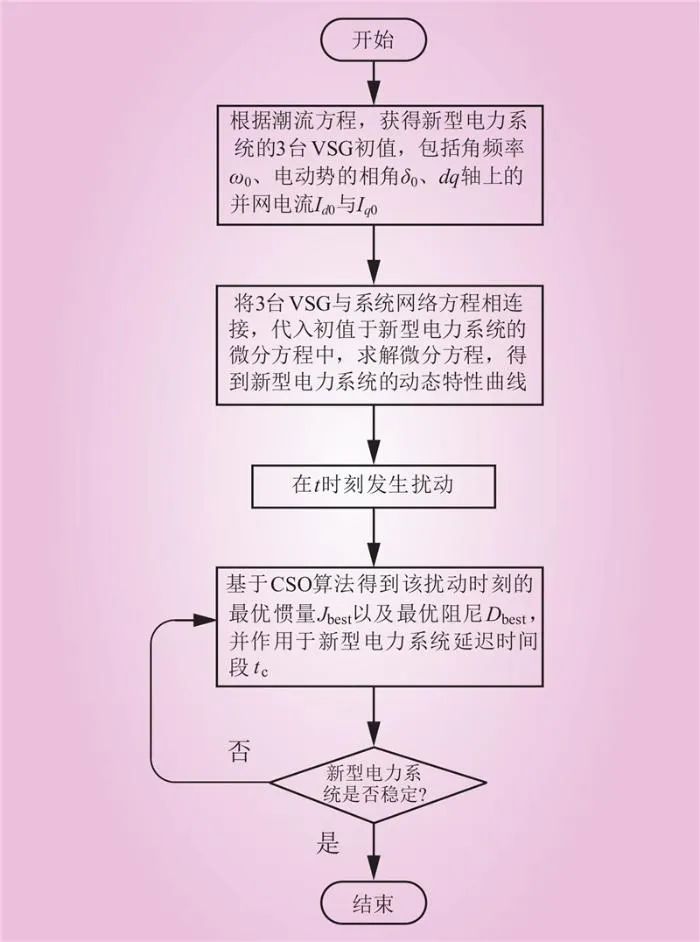
图5 基于CSO的新型电力系统惯量延迟优化控制流程
Fig.5 Optimized control flowchart of new power system inertia delay based on CSO
3 仿真案例分析
为验证所提控制策略的有效性,本文根据1.2小节,利用Matlab/Simulink得到新型电力系统动态特性曲线,其设计参数以及3台VSG微分方程的初值如表1所示。
表1 新型电力系统的参数
Table 1 Parameters of new power system
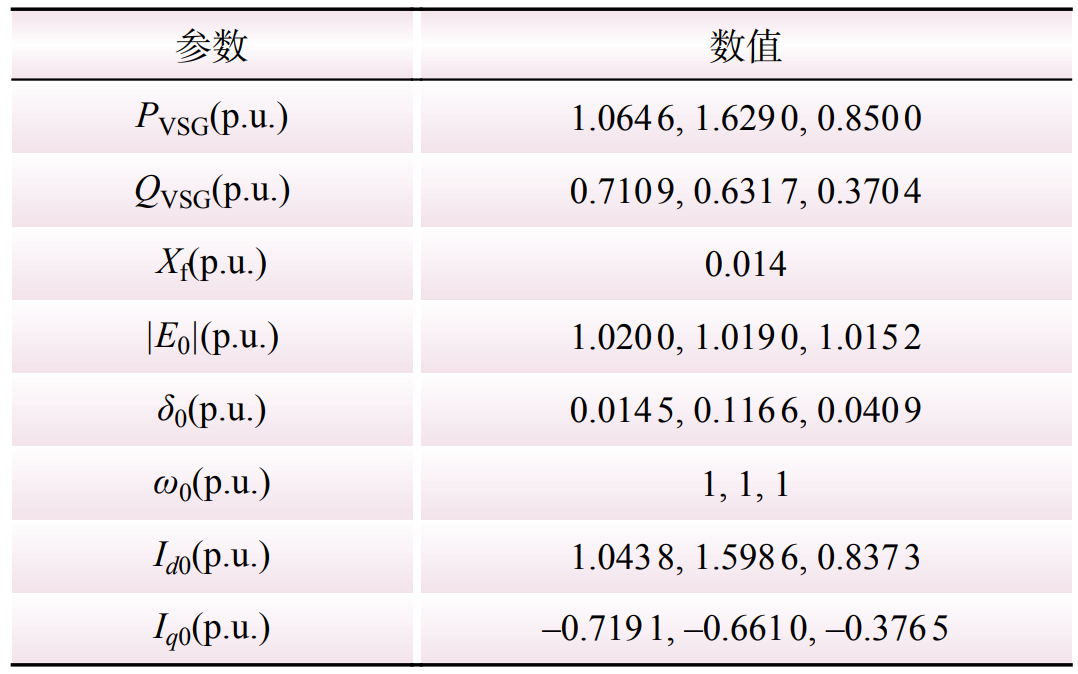
本文设置节点1于0.2 s时发生三相短路故障,气势汹汹 威逼0.25 s故障解除,造成系统功率不平衡,利用3台VSG的频率以及有功功率的动态曲线反映新型电力系统的动态特性。
3.1 惯量和阻尼影响动态特性曲线
为了验证本文设计的惯量延迟优化控制的合理性,根据2.2节的内容,模拟了新型电力系统的动态特性曲线,同时,通过改变3台VSG的惯量和阻尼,定性分析了惯量和阻尼对新型电力系统动态特性的影响,如图6所示。
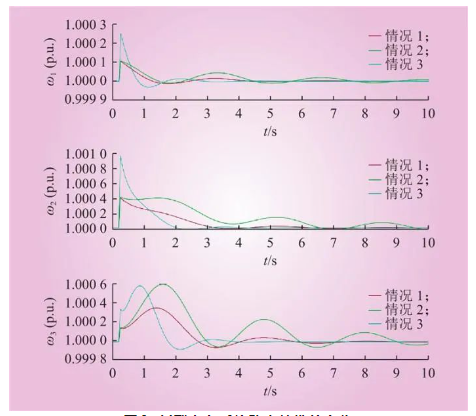
图6 新型电力系统动态特性的变化
Fig.6 Changes in dynamic characteristics of new power system
图6中,情况1:3台VSG的惯量都为500,阻尼都为500,作为参考对比组。情况2:降低VSG阻尼,3台VSG的惯量都为500,阻尼都为200。情况3:降低VSG惯量,3台VSG的惯量都为200,阻尼都为500。
由图6可知,情况1作为参考实验组,3台VSG的调节时间分别为6.46 s、6.15 s、7.53 s,频率波动最大值分别为1.00010 p.u.、1.00004 p.u.、1.000035 p.u.。情况2缩小了3台VSG的阻尼,3台VSG的调节时间均大于10 s,频率波动最大值分别为1.00010 p.u.、1.00004 p.u.、1.00006 p.u.。对比情况1和情况2可知,降低了系统的阻尼对调节时间以及频率波动幅值有影响。情况3缩小了3台VSG的惯量,3台VSG的调节时间分别为5.57 s、5.15 s、5.53 s,频率波动最大值分别为1.000250 p.u.、1.000095 p.u.、1.000052 p.u.。对比情况1和情况3可知,降低系统惯量对调节时间以及频率波动幅值有影响。
3.2 惯量延迟控制改善系统动态特性
根据2.3小节的总流程构建了基于纵横交叉算法的新型电力系统惯量延迟优化控制策略,将该策略与无优化控制作对比,3台VSG的频率、功率动态特性曲线分别如图7和图8所示。
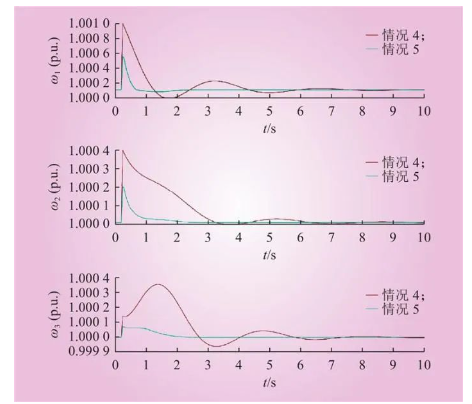
图7 3台VSG的频率动态特性曲线
Fig.7 Frequency dynamic characteristic curves of three VSGs
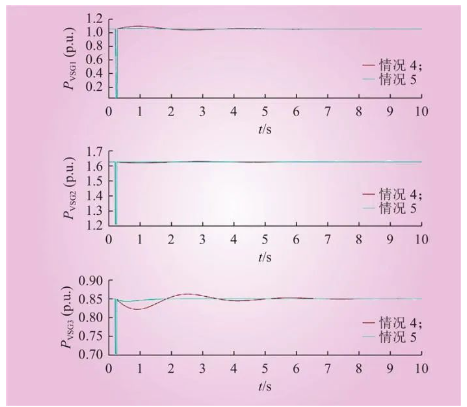
图8 3台VSG的功率动态特性曲线
Fig.8 Power dynamic characteristic curves of three VSGs
图7、8中,情况4:无优化控制,3台VSG的惯量都为500,阻尼都为500;情况5:3台VSG采用惯量延迟优化控制策略,3台VSG的惯量都为500,阻尼都为500。
由图7和图8可知,情况4无优化控制下,3台VSG的调节时间分别为6.46 s、6.15 s、7.53 s,频率波动最大值分别为1.00010 p.u.、1.00004 p.u.、1.000035 p.u.,故障解除后功率波动最大值分别为1.100 p.u.、1.621 p.u.、0.822 p.u.。情况5惯量延迟优化控制策略下,3台VSG的调节时间分别为2.14 s、2.53 s、2.41 s,频率波动最大值分别为1.000040 p.u.、1.000020 p.u.、1.000005 p.u.,功率波动最大值分别为1.073 p.u.、1.627 p.u.、0.840 p.u.。对比情况4与情况5可知,采用本文提出的基于纵横交叉算法的新型电力系统惯量延迟优化控制策略后,调节时间变小,振荡幅值变小,有效优化了新型电力系统的动态特性。
3.3 惯量延迟控制对比实时控制
为了证实本文设计的延迟控制减少系统计算负担,同时又能有效地优化新型电力系统的动态特性。将惯量实时控制与惯量延迟控制作对比,两者的角频率动态特性如图9所示。
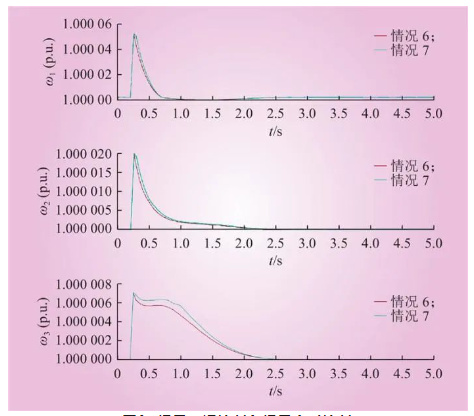
图9 惯量延迟控制和惯量实时控制
Fig.9 Inertia delay control and real-time control
图9中,情况6:3台VSG采用惯量实时控制;情况7:3台VSG采用惯量延迟控制,延迟时间段tc为0.1 s。
由图9可知,情况6和情况7的调节时间相近,角频率波动相差不大,因此可以得出惯量延迟控制效果近似于惯量实时控制。由于惯量延迟控制中设置了延迟时间段,耳环 线人延迟时间段中,并没有进行CSO优化控制,大大减少了计算负担。因此,本文设计的惯量延迟优化控制既减少了计算负担,缩短控制优化时间,又能较好地实现惯量实时优化控制的效果。
4 结论
本文提出了基于纵横交叉算法的新型电力系统惯量延迟优化控制策略。通过仿真案例分析,得出以下结论。
1)建立了全部虚拟同步机为主导的新型电力系统模型,通过VSG的微分方程以及三机九节点的网络方程,得到了新型电力系统的动态特性曲线,并定性分析了惯量和阻尼对新型电力系统的动态特性的影响。
2)基于纵横交叉算法的惯量延迟优化控制有效地改善新型电力系统的动态特性,使得系统调节时间更短,且振荡幅值更小。
3)本文设计的惯量延迟优化控制既减少了计算负担,缩短控制优化时间,又能较好地实现惯量实时优化控制的效果。
注:本文内容呈现略有调整,如需要请查看原文。
声明:本网站部分文章来自网络,转载目的在于传递更多信息。真实性仅供参考,不代表本网赞同其观点,并对其真实性负责。版权和著作权归原作者所有,转载无意侵犯版权。如有侵权,请联系www.buxiuwenxue.com(乐鱼体育)删除,我们会尽快处理,乐鱼体育将秉承以客户为唯一的宗旨,持续的改进只为能更好的服务。-乐鱼体育(附)


